A couple of weeks ago I got interested in this project but wanted full control of the code, wanted to know exactly what it is doing, wanted a bunch of features like the ability to import and export CA rules, and wanted to have the process not be seeded by cellular automata already featuring gliders (which the web app seems to be). To this end I have pushed a project to github that does something similar but, I hope, more transparently.
I’m calling it Lifelike Cellular Automata Breeder. It is a (C# WinForms) application in which given some settings a user can artificially select and breed cellular automata; i.e., it performs a genetic algorithm in which the user manually provides the fitness criteria interactively.
I decided I wanted to only allow a reproduction step in which I scramble together state tables in various ways, guessing that using “DNA” more complex than commensurate 2D tables of numbers wouldn’t work well for a genetic process in this case. I characterize CA rules as applying only relative to a given number of states and a given, what I call, “cell structure” and “neighborhood function”. Cell structure just means a lattice type and neighborhood –e.g. square, with four neighbors; square, with eight neighbors; hex, with six, etc. “Neighborhood function” is an arbitrary function that given the states of the n cells in some cell’s neighborhood returns an integer from 0 to r where r is dependent on the neighborhood function and possibly number of states. For example, Conway Life uses the neighborhood function I refer to as “alive cell count”, and for an n-cell neighborhood, r equals n because the greatest number of alive cells that can surround a cell is just the size of the neighborhood. If the user has selected s total states, the state tables will be s by r.
Lifelike works as follows
- The user selects a number of states, cellular structure, and neighborhood function and kicks off the genetic process.
- Lifelike sets the current generation to nil, where by “generation” we just mean a set of cellular automata that have been tagged with fitness values.
- While the user has not clicked the “go to the next generation” button,
- If the current generation is nil, Lifelike randomly generates a cellular automata, CA, from scratch by making an s by r state table filled with random numbers from 0 to s. (The random states are generated via a discrete distribution controllable by the user). If the generation is not nil, Lifelike selects a reproduction method requiring k parents, selects k parents from the current generation such that this selection is weighted on the fitness of the automata, generates CA using the reproduction method and parents, and then possibly selects a random mutation function and mutates CA, selecting the mutation function via a discrete distribution controllable by the user and applying it with a “temperature” controlled by the user.
- Lifelike presents CA in a window.
- The user either skips CA in which case it no longer plays a role in the algorithm or applies a fitness value to it and adds it to the next generation.
- When the user decides to go to next generation, the selections the user just made become the new parent generation and processing continues.
Here’s a video of me playing with an early version of the application.
Results, Musings, etc.
Briefly, Lifelike works.
You can produce interesting cellular automata with it and there is a weird feeling that is hard to describe when you first see a tiny glider wiggle across the screen; however, the way it works is somehow more mundane than I thought that it would be. I wonder if all genetic algorithms are like this. Most of what it produces is garbage. When you see something that isn’t garbage you can select for it. However Lifelike doesn’t do magic. It doesn’t magically find phenomena you want just because you have a fancy framework implemented to find such phenomena. For example, it is my belief at this point that there is no simple hex grid analog of Conway Life using alive cell count, a six cell neighborhood, and 2-states. I think you could probably prove the non-existence of gliders in this configuration but it would be a boring proof by exhaustion and running Lifelike on that configuration is boring as well. Just because you, the user, are a step in a “genetic algorithm” doesn’t somehow make it interesting.
The simple hex neighborhood negative result led me to ask the following question: What is the smallest change you can make to hex/6-cell/alive cell count/2 states to allow Conway Life-like behavior? If you google “Hex Life” you will find that it is well-known that interesting things can happen if you go to a 12-cell Star of David shaped neighborhood, but this seems inelegant to me because the simple hex neighborhood is so nice. The question then is are gliders possible in the simple hex lattice and neighborhood if we add one state and modify “alive cell count” in a trivial way? The answer to this question turns out be yes. There are beautiful rules that live in the hex lattice with the natural neighborhood if we have 0 = death, 1 = Alive-A, 2 = Alive-B and instead of the simple alive cell count we use its natural analog when states can have values greater than one: sum of states.
Below is a such a rule set and is probably the best thing that has come out of my work with Lifelike as far as I am concerned (So I am naming it Joe Life, assuming that it is unknown in the literature).

The above has a nice quality that Conway Life also has that I call “burn”. This a qualitative thing that is really hard to define but it is what I look for now when I play with Lifelike: burn + gliders = a Life-like cellular automaton. “Burn” is the propensity of a cellular automata configuration to descend into segregated regions of chaos that churn for awhile before ultimately decaying into gliders, oscillators, and still lifes. Some CAs burn faster than others; the above has a nice slow burn. CAs that exhibit steady controlled burn turn out to be rare. Most CAs either die or devolve instantly into various flavors of unbounded chaos.
However there does turn out to be another quality that is not death or unbounded chaos that is sort of like the opposite of burn. See for example

(The above is hex 6-cell, four states, and using a neighborhood function I call “state-based binary”) which I have been calling “Armada” and generally have been referring to these kind of CAs as being armada-like. Armada-like cellular automata quickly decay completely into only weakly interacting gliders. For example, one from the literature that I would characterize as armada-like is Brian’s Brain. Armada-like rules turn out to be more common than life-like rules. They’re impressive when you first start finding them but they are ultimately less interesting, to me at least. The best thing about armada-like rules is that they indicate that life-like rules are probably “nearby” in the space you are exploring in the genetic process.
Also they can breed weird hybrids that defy classification, such as the following which are all burn with large blob-like gliders and seem sometimes to live around the boundary between armada-like rules and life-like rules.
Magic Carpets (square, 4-cell/ 4 states / sum of states)
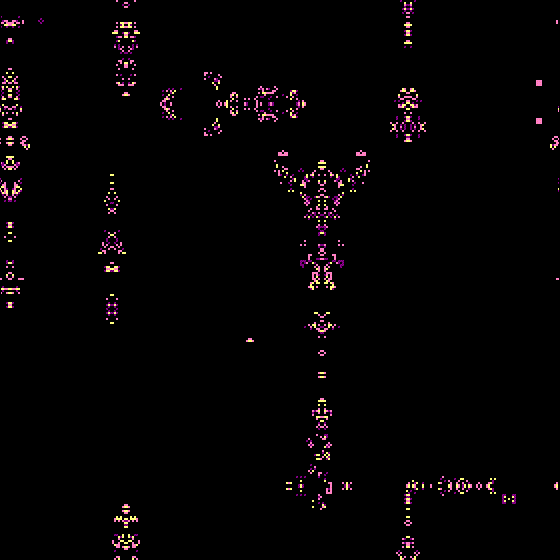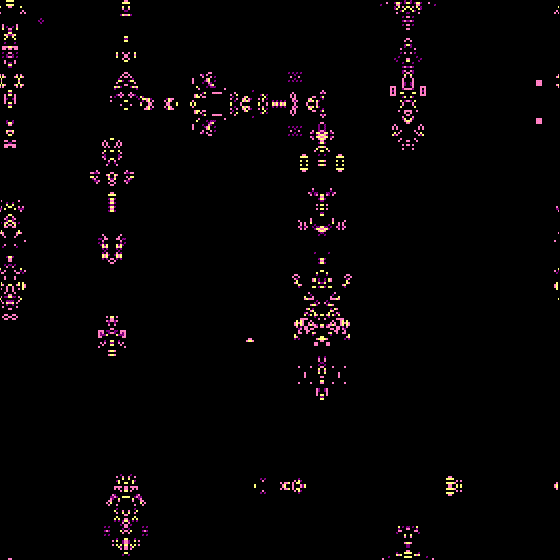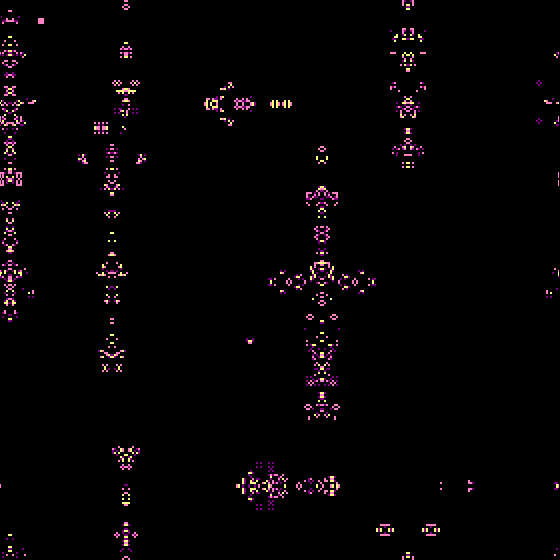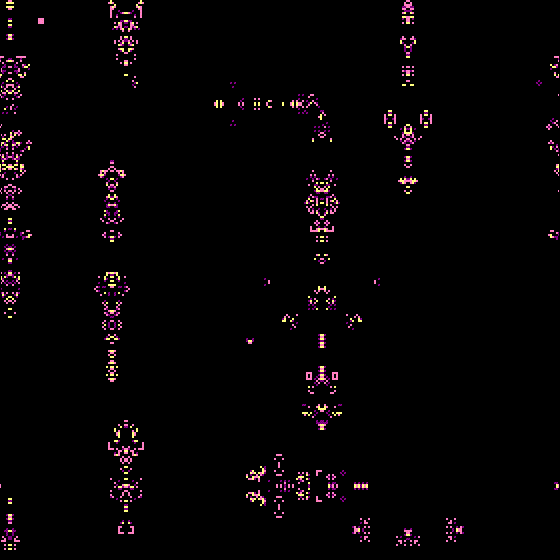
or Ink Blots (hex, 6-cell/ 3 states / “0-low-med-high”)

My other major result is that life-like rules exist in the square 4-cell neighborhood if we allow an extra state and use the simple sum of states as the neighborhood function, but they can be boring looking so instead here is an armada-like square 4-cell CA that is on the edge of being lifelike:

The above uses the neighborhood function I call “2-state count” which enumerates all possible combinations of c1, number of neighboring cells in state 1 and c2, number of neighboring cells in state 2 or above, in an n-cell neighborhood i.e. c1 + c2 ≤ n.



Pingback: The Curiously Recurring Gimlet Pattern » Is their hexagonal analog of Conway’s Game of Life?
Your hex CA is amazing, but what about glider guns? Conway said, “When we discovered glider guns we knew we were really onto something.” Interference between guns is like a transistor. You’re halfway to a Turing machine when you find guns.
What about traversing the tree of backward possible states to automatically search for glider guns? Then run them forward and look for glider streams.
What about Wolfram style rules for triangles? You only need 1 more cell, but you need a bit for triangle orientation, a quantum spin state. That’s 256^4, 65536×65536 bitmap, or 1626^3. You can divide axes by spin for the bitmap, and for 3D take sum of all adjacent triangles from all rules turned “on” (taken to the power of 2 of each rule value), with spin changing the sign.
I’d love to see 256^3 cubic slices of the 256^4 parameter space with transparent colored surfaces separating regions with different #’s of guns.